本文学习任意风格只需要训练一个WCT模型,而且训练过程中不需要风格图的风格转换论文"Universal Style Transfer via Feature Transforms"。
作者 Code
Authors:Yijun Li, Zhaowen Wang, Chen Fang, Xin Lu, Jimei Yang, Ming-Hsuan Yang
2017 NIPS
Abstract
目前的基于前馈的方法,推断时很有效,但是对于未见过的风格无法有效进行推断,或者在图片质量上妥协。我们提出一种简单有效,不需要在预先定义的风格图上训练的方法。关键的组成部分是被用于图片重建网络的一对特征转换,whitening和coloring。
whitening 和coloring 转换反映了内容图和给定风格图特征协方差的直接匹配,这和优化Gram矩阵来进行风格转换有相似的思想。
Introduction
主要挑战是如何提取风格图的有效表示,然后将其匹配到内容图中。
Gram矩阵和协方差矩阵可以很好的刻画特征之间的关系,所以被用来捕获视觉风格特征。
基于优化的方法可以处理任意风格的图片,并得到令人满意的结果,但是计算量巨大。基于前馈的方法可以很快得到转换后的图片,但是只能应用于固定数量的风格,或者在图片质量上妥协。
在每一个中间层,我们的目标是转换提取的内容特征,使得它们和相同层的风格特征有一样的统计特性。我们发现在这些特征上做经典的WCT转换可以实现这一目标。
我们首先利用VGG-19进行特征提取(encoder),然后训练一个对称decoder来反转VGG-19特征到原始图片,本质上就是重建图片。一旦训练完成,encoder和decoder网络在整个实验中就固定不动了。
为了进行风格转换,我们对内容特征的某一层应用WCT,使得其协方差矩阵和风格特征的协方差矩阵匹配。转换后 的特征作为decoder层的输入以获得风格化后的图片。除了单层风格化,还有多层风格化pipeline,其效果比单层的好。
当给一个新的风格图时,我们不需要对风格图在已有的风格基础上进行微调,而是提取特征协方差矩阵,然后将它们通过WCT应用到内容特征上。
本文主要算法结构如下:
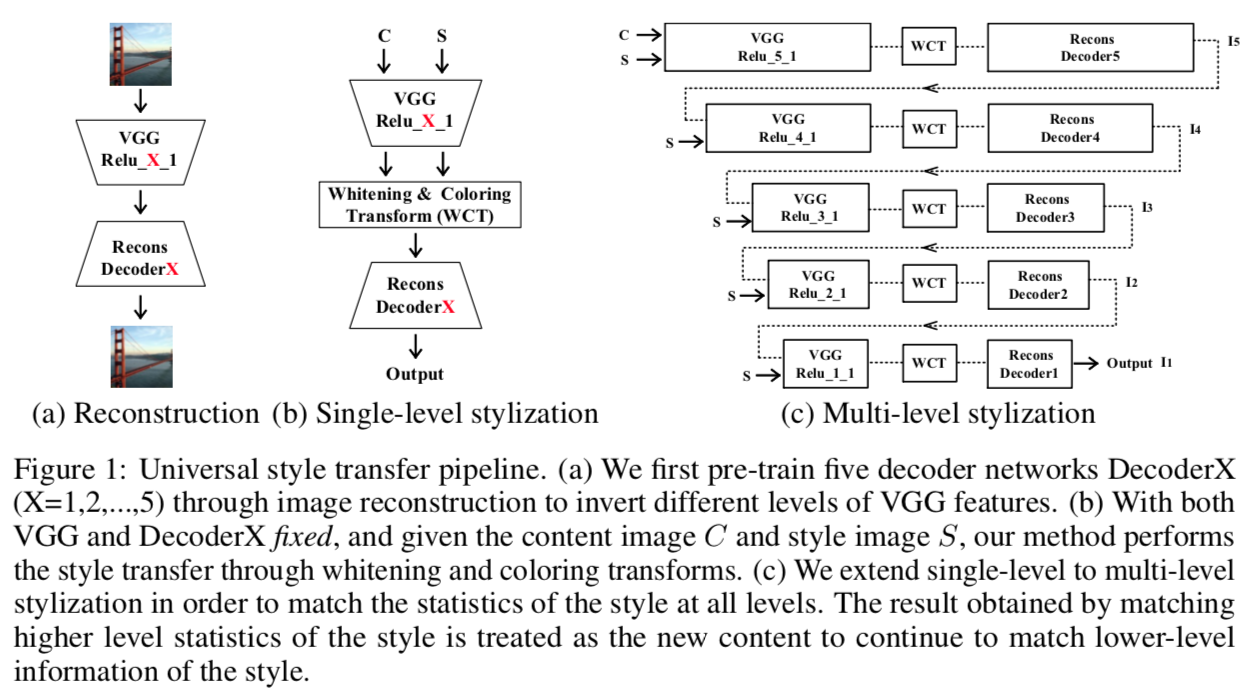
Proposed algorithm
我们将风格转换表示为用特征转换(如WCT)进行图片重建的过程。
reconstruction decoder
decoder被设计为与VGG-19对称的
loss为:
$$ L = ||I_o - I_i|| _2 ^2 + \lambda || \Phi (I_o) - \Phi (I_i) || _2 ^2 $$
whitening and coloring transforms
本节用到的一些符号解释
| 符号 | 含义 |
|---|---|
| $ I_c $ | 内容图 |
| $ I_s $ | 风格图 |
| $ f_c \in R ^{ C × H_c W_c } $ | 内容图的VGG特征, $ H_c $ 和 $ W_c $ 分别代表内容特征的高和宽, $ C $ 是channel数 |
| $ f_s \in R ^{ C × H_s W_s } $ | 风格图的VGG特征 |
| $ \hat f_c $ | 白化特征 |
将 $ f_c $ 直接喂给decoder,decoder将重构原始图片 $ I_c $ 。接下来我们将使用WCT相对 $ f_s $ 的统计调整 $ f_c $ 。WCT的目标是直接转化 $ f_c $ 以匹配 $ f_s $ 的协方差矩阵。包含两步:whitening transform和coloring transform。
Whitening transform
在whitening之前,首先通过减去 $ f_c $ 的均向量 $ m_c $ 来集中 $ f_c $ ,然后将 $ f_c $ 进行如下线性转换得到 $ \hat f_c $ 使得特征之间是不相关(即正交矩阵)的( $ \hat f_c \hat f_c^T = I $ ,转置=逆 的矩阵为正交矩阵)。 $$ \hat f_c = E_c D _c ^{ - \frac {1}{2} } E_c^T f_c $$ $ D_c $ 是协方差矩阵 $ f_c f_c^T \in R ^{C × C} $ 特征值的对角矩阵, $ E_c $ 是对应特征向量的正交矩阵,满足 $ f_c f_c^T = E_c D_c E_c^T $ 。
解读上式
协方差矩阵的 $-\frac {1}{2} $ 方*矩阵=每行均变为均值为0,方差为1的向量
$ f_c f_c^T $ 为协方差矩阵,求其 $ - \frac {1} {2} $ 方,不太好求得,所以对其进行对角线分解,对得到的对角矩阵进行分解,得到 $ f_c f_c^T = E_c D_c E_c^T $ ,其中 $ (E_c D_c E_c^T) ^{-\frac {1}{2}} = E_c D_c ^{ - \frac {1}{2} } E_c^T $ 。
为了验证白化特征 $ \hat f_c $ 中编码了哪些信息,我们用我们之前训练好的decoder将其反转到RGB空间。图2显示白化之后的特征依然保留了图内容的全局结构,但是移除了其他与风格相关的信息。
Coloring transform
首先减去 $ f_s $ 的均向量 $ m_s $ 来集中 $ f_s $ ,然后执行coloring 转换,即对 $ \hat f_c $ 进行线性变换,其本质上是whitening步的逆步骤。这样,我们就能得到特征之间有着需要关系的 $ \hat f_{cs} $ ( $ \hat f_{cs} \hat f_{cs} ^T = f_s f_s^T $ )。
$$ \hat f _{ cs } = E _s D _s ^{ \frac { 1 } { 2 } } E _s ^T \hat f _c $$
$ D_s $ 是协方差矩阵 $ f_s f _s ^T \in R ^{ C × C } $ 特征值的对角矩阵, $ E_s $ 是对应特征向量的正交矩阵。
最后,给 $ \hat f _{ cs } $ 加上均向量 $ m_s $ 进行去中心化, $ \hat f _{ cs } = \hat f _{cs} + m_s $
经过WCT变换后,在将其输入到decoder之前,将 $ \hat f _{ cs } $ 和 $ \hat f _{ c } $ 进行线性组合,方便用户控制风格化效果的程度。
$$
\hat f _{ cs } = \alpha \hat f _{cs} + ( 1- \alpha ) f_c
$$
$ \alpha $ 为风格权重。
multi-level coarse-to-fine stylization
coarse-to-fine风格化中,高层特征捕捉风格的显著特征,低层特征增强细节。如果换成fine-to-coarse,低层信息在经过高层特征之后无法保留。
Experimental results
decoder training
dataset:MSCOCO
style transfer
- DeepArt:基于优化,可以处理任意的风格,但很可能遇到局部极小值问题
- TNet:风格化速度提高了,但是为了效果,其在质量和通用性之间做了权衡,使得其会产生相同内容覆盖的重复模块
- style-swap:能力有限,当风格在低阶信息(颜色)中很难反映时,内容特征会被严格保留
- Huang:内容特征仅仅用来被调整以获得和风格特征相同的均值和方差,对于获得风格图的高阶表示是无效的。对于未见过的风格图没有通用性。对于捕获并合成显著风格模式是无效的,尤其是有着丰富局部特征和非平滑区域的复杂的风格。
- 我们的方法:没有学习任何风格,我们的模型可以捕获风格图中明显的外观模式。此外,内容图中的主要部分在我们的模型中可以被风格化,其他方法只能转化相对平滑的区域。
- 用协方差矩阵来定量分析风格化图片和风格图的差异
user study
efficiency
在WCT中有一个特征值分解步,但随着图片size的增加,这一步的计算开销并不会随之增大,因为协方差矩阵的维度只取决于filter channels的数量,最大也就是512(Relu_5_1)。
user control
不仅仅能进行风格转换,还能满足用户的不同风格化需求,如:
1. 大小:调整风格图输入的size
2. 权重:风格图和内容图占比,不需要重新进行优化,直接计算
3. 空间控制:内容图的不同部分用不同风格进行转换,需要输入额外的masks M
texture synthesis
通过将内容图设置为随机噪声图(如高斯噪声),我们的风格化框架可以将其应用为纹理合成,或者可以直接将 $ \hat f_c $ 初始化为白噪声,两种方法能得到相同的结果。
经验结果:运行几次多层pipeline可以得到令人视觉上满意的结果。
我们的方法也能将两种纹理进行结合,生成新的纹理效果。
可生成多样性的纹理合成结果

