style_swap

  本文学习任意风格只需要训练一个style-swap模型的风格转换论文"Fast Patch-based Style Transfer of Arbitrary Style"。

  这是Torch Code 作者源码
  Authors ：Tian Qi Chen ，Mark Schmidt
  publication in 2016

Abstract

现有问题

  1. 对所有风格图均有效，但很贵
  2. 或者只对有限的被训练过的风格图有效

本文工作

• 本文提出基于本地匹配的一种简单的优化目标：在预训练网络的某一层结合内容结构和风格纹理
• 我们的目标有令人满意的属性如简单的优化景观、直觉参数调整和在视频中一致的逐帧性能。
• 程序对任意内容和风格图都适用

Introduction

  一个经典的加速加速解决方案：训练另一个神经网络，该神经网络近似于单个前馈神经网络传递优化中的最优值。然而，目前的工作牺牲了通用性，因为前馈神经网络无法推广到训练集中没有出现过的图片。
  因此，目前的应用，要不就耗时比较长，要不就只能提供有限风格的转化。
  本文提出一个仅仅依赖于CNN某一层的新的优化目标，目前的方法使用CNN中的多层。新的目标函数使得我们使用“inverse network”确切地在风格化层逆转激活函数，然后产生风格化之后的图片。

Related work

Style Transfer as Optimization

  速度慢

Feed-forward Style Networks

  对于每一种新的风格图需要重新训练

Style Transfer for Video

Inverting Deep Representations

  为了与已有风格转化方法进行对比，我们提出一种方法，直接重构预训练好的CNN网络中某一层的目标激活函数。
  像Li和Wand一样，我们使用一个标准在激活函数空间寻找最佳匹配patch。但是我们的方法直接构建整个激活目标。这个确切的过程使得我们的方法很容易应用到视频中，而不用考虑一致性问题。
  我们不用像素级别的loss，而是在激活函数上使用loss。
  在特定的训练设置下，逆转网络甚至可以逆转一般CNN激活函数范围之外的激活函数

A new objective for style transfer

  同样基于预训练好的VGG网络，在某一ReLU激活层进行基于patch的交换操作：将内容图片的每一个patch用与其最接近的风格patch代替。
  本文主要算法结构如下：

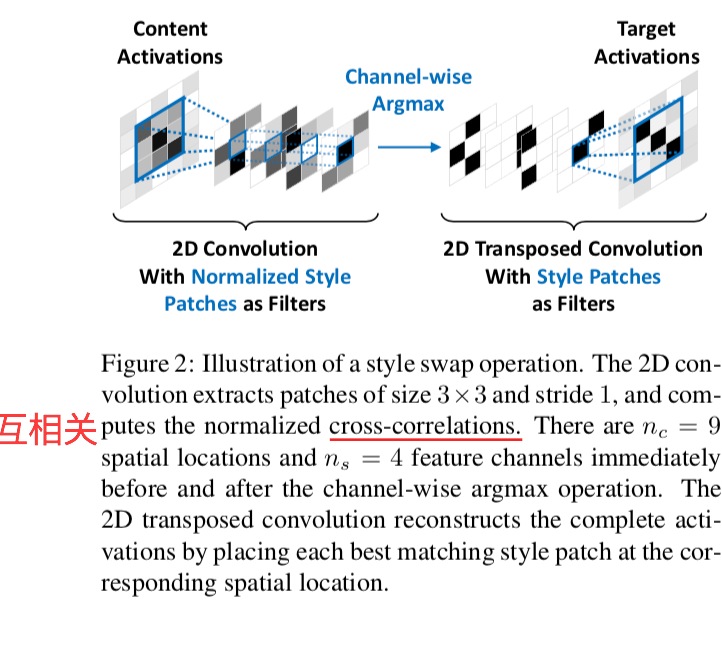
Style swap

本节用到的一些符号解释

符号	含义
$ C $	内容图的RGB表示
$ S $	风格图的RGB表示
$ \Phi( \cdot ) $	将一幅图用预训练好的VGG网络从RGB表示转换为某些中间激活层的转换函数
$ \Phi( C ) $	内容图的激活层表示
$ \Phi( S ) $	风格图的激活层表示
$ \phi _i ( C ) $	内容图在位置$ i $的激活函数patch
$ \phi _i ( S ) $	风格图在位置$ i $的激活函数patch
$ \phi _{a,b} ( C ) $	内容在位置$ a,b $的激活函数patch：$ \Phi ( C ) _{a:a+s,b:b+s,1:d} $,其中$ s $代表patch size
$ \phi _i ^{SS} ( C,S ) $	与内容图激活patch$ i $最接近的风格patch
$ \Phi ^{SS} ( C,S ) $	重构的完整内容图激活层

交换过程如下

1. 对内容图和风格图分别提取patch，分别用$ { \phi _i ( C ) } _{i \in n_c} $ $ { \phi _i ( S ) } _{i \in n_s} $表示，其中$ n_c $ $ n_s $为提取的patch。提取的patch应该有足够多的重叠，并包含所有激活函数channel
2. 对于每个内容激活patch，基于归一化互相关度量方法，得到与其最接近的风格patch $$ \phi _i ^{SS} ( C,S ) := \mathop {\arg \max} _{\phi _j ( S ), j=1, \cdots , n_s} {\dfrac {<\phi _i ( C ), \phi _j ( S )>} {||\phi _i ( C )|| \cdot ||\phi _j ( S )||} } \text{ (1) } $$
3. 将每个内容激活patch $ \phi _i ( C ) $，用与其最接近的风格patch$ \phi _i ^{SS} ( C,S ) $替换
4. 重构完整的内容图激活层，用$ \Phi ^{SS} ( C,S ) $表示，重叠部分取平均值

  这样就能得到一个既有内容图的结构，又有风格图的纹理的图片的隐藏激活层。

parallelizable implementation

  因为对于每一个内容激活函数patch的argmax操作，其归一化项是个常数，所以式(1)可以重写为

$$ K _{a,b,j} = <\phi _{a,b} ( C ), \frac {\phi _j ( S )} {||\phi _j ( S )|| } > $$

$$ \phi _{a,b} ^{SS} ( C,S ) = \mathop {\arg \max} _{ \phi _j ( S ),j \in N_s } { { K _{a,b,j} } } $$   内容激活函数patch归一化项的缺失可简化计算，且使得我们可以直接使用2D卷积层。

实现步骤

1. 2D卷积层：$ K $ 可以用归一化后的风格激活函数patch $ \left( \dfrac { \phi _j ( S ) } { || \phi _j ( S ) || } \right) $ 作为卷积层， $ \Phi ( C ) $ 作为输入进行卷积操作得到。计算结果 $ K $ 有 $ n_c $ 个空间位置， $ n_s $ 个feature channels。在每个空间位置， $ K _{ a,b } $为内容激活函数patch和所有的风格激活函数patch之间的互相关向量。
2. channel-wise的argmax：将$ K_{a,b} $用一个one-hot向量代替 $$ \overline{K} _{a,b,j} = \begin{cases} 1, & \text{if $j = \mathop {\arg \max} _{ j^{'} { K _{a,b,j^{'}} } } $ } \ 0, & \text{otherwise} \end{cases} $$
3. 2D转置卷积层：将$ \overline{K} $作为输入，未归一化的风格激活函数patchs $ { \phi _j ( S ) } $作为filter进行转置卷积操作。在每个空间位置，只有最匹配的风格激活函数patch在输出中，其他的patch乘以0。

optimization formulation

  合成图表示可以通过在目标激活函数$ \Phi ^{SS} ( C,S ) $上的loss来计算得到。

$$ I _{stylized} ( C,S ) = \mathop { \arg \min } _{ I \in R ^{ h×w×d } } { || \Phi (I) - \Phi ^{ SS } ( C,S ) || _F ^2 + \lambda l _{TV} (I) } $$   合成的图的size为$ h×w×d $，$ || \cdot || _F $ 代表Frobenius范数，$ l _{TV} (\cdot) $ 代表total variation（全变分）正则项。

Inverse network

  inverse network的主要目的是对于任意目标激活函数，近似损失函数的最优值，因此我们定义优化逆转函数为

$$ \mathop { \arg \min } _{ f } E _H \left [ || \Phi ( f(H) ) - H || _F ^2 + \lambda l _{ TV } ( f(H) ) \right] $$

   $ H $ 代表目标激活函数，$ f $ 代表逆转神经网络。

Training the Inverse Network

  由于预训练好的卷积网络，有两个问题

1. 非单射：CNN中的卷积层、maxpooling、和ReLU层都是多对一的，因此没有合适的逆运算。类似于已有的工作，我们不训练逆转关系，而是训练一个参数化的神经网络 $$ \min _{ \theta } \dfrac { 1 } { n } \sum _{ i=1 } ^n \left [ || \Phi ( f( H_i ; \theta ) ) - H_i || _F ^2 + \lambda l _{ TV } ( f( H_i ; \theta ) ) \right ] $$  $ \theta $ 代表逆转神经网络 $ f $ 的参数， $ H_i $ 代表有 $ n $ 个样本的数据集中的激活函数特征。
2. 非满射：如果逆转网络仅仅只训练了真实图片，那么逆转网络可能只能逆转在$ \Phi( \cdot ) $范围内的激活函数。鉴于我们希望逆转风格交换后的激活函数，所以我们增强训练数据集以包含这些激活函数值。

Feedforward Style Transfer Procedure

风格转换过程

1. 计算$ \Phi( C ) $和$ \Phi( S ) $
2. 通过风格交换获得$ \Phi ^{SS} ( C,S ) $
3. 将$ \Phi ^{SS} ( C,S ) $喂入训练好的逆转网络

Experiments

Style Swap Results

• 目标层为relu3_1是效果最好
• 训练更少轮便能到达最优点
• 随机初始化对结果影响不大
• 比其他现有目标函数少很多局部极小值
• 一致性：可以直接应用到视频中，而不用任何类似光流的粘合

CNN Inversion

• $ \lambda = 10 ^{-6} $
• Adam
• learning_rate:$ 10 ^ {-3} $
• 数据增强的效果好于未增强的效果

Computation Time

• 时间大多花费在风格交换步
• 图片越大，花费时间越长

参考

  Fast Patch-based Style Transfer of Arbitrary Style